
The site's hierarchy
Navigation
| M | T | W | T | F | S | S |
|---|---|---|---|---|---|---|
| 23 | 24 | 25 | 26 | 27 | 28 | 1 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | 1 | 2 | 3 | 4 | 5 |
- Les premiers zoom de galaxies sont accessibles
- Le halo FOF 6133 de la boite Horizon L et le halo FOF 544 de Horizon S ont été resimulés avec plusieurs techniques de zoom. Il est important que chaque "zoomer" valide sa méthode, avant de lancer une campagne de zoom sur un plus grand cataloque.
- Les données de la simulation Mare Nostrum sont disponibles
- 34 snapshots jusqu’à z=4 sont accessibles sur horizon3 et sur le serveur de fichiers de l’IDRIS à la collaboration Horizon.
- Méso Machine HPC1 opérationnelle
- Depuis le 23 Octobre 2005, la Méso machine du site horizon est operationnelle. Elle correspond à 3 quadriprocesseurs avec chacun 64 Giga de RAM reliés par infiniband, ainsi qu’un access conséquent (sur une base de projet dédié) au reste de la ferme). Son acces est ouvert a toute personne de la collaboration ayant acces à la minigrille et qui en fait la demande a admin-minigrille
- http://
- Workshop Horizon le 14 et 15 novembre 2005
- Il aura lieu à Paris les 14 et 15 novembre 2005 (prévoir une nuit sur place). L’enregistrement est ouvert dans la rubrique "meeting!"
- http://
Quintessence et formation des structures
Note
Cet article résume des résultats obtenus par le noeud du LUTh au sein du projet HORIZON (J.-M. Alimi, A. Füzfa, F. Roy - LUTh, Observatoire de Paris-Meudon ; V. Boucher (CP3, Université Catholique de Louvain, Belgique). Les simulations PM matière noire avec 1024^3 particules ont été générées à l’IDRIS sur le serveur Zahir (IBM eServer p690, p690+ et p655 ; Regatta Power4) dans le cadre du projet 1034 (un merci tout spécial à J. Devriendt pour ses heures de calcul et ses encouragements).
Les modèles de quintessence
Pour rappel, la quintessence est un avatar dynamique de l’énergie noire contrairement à l’habituelle constante cosmologique dont la densité d’énergie demeure constante au cours du temps. La quintessence, “cette constante cosmologique variable”, est non seulement motivée par de nombreux modèles de physique des hautes énergies mais permet également de palier aux problèmes épineux de la constante cosmologique que sont ceux de l’ajustement fin et de la coïncidence cosmique.
La quintessence est le plus souvent modélisée par un champ scalaire de masse très faible qui n’est ressenti par la matière ordinaire uniquement par l’intermédiaire indirect de la gravitation (on parle de “couplage minimal”) principalement par la modification de l’expansion cosmique qu’elle induit. A la différence de la constante cosmologique, la quintessence est non seulement variable dans le temps mais également dans l’espace (inhomogénéité) ce qui implique de fortes contraintes sur son couplage direct à la matière (qui entraînerait alors une violation du principe d’équivalence). Cette propriété d’inhomogénéité constitue une des empreintes essentielles de la quintessence par rapport à la constante cosmologique.
Dans ce travail, nous avons considéré deux modèles de quintessence sous la forme de champs scalaires dont les potentiels d’auto-interaction sont ceux de Ratra-Peebles (puissance inverse du champ, P.J.E. Peebles, B. Ratra, ApJ 325 (1988)) et ce même potentiel affublé d’une correction supergravifique (P. Brax, J. Martin, Phys. Rev. D 61 103502 (2000)). Ces modèles sont bien connus pour exhiber des propriétés de “tracking”, c’est-à-dire un mécanisme expliquant naturellement la coïncidence cosmique indépendamment des conditions initiales. La figure 1 donne une idée de la variation de l’équation d’état de la quintessence (rapport p/rho) pour les modèles de Ratra-Peebles (RPCDM) et Sugra (SUCDM) durant l’ère dominée par la matière.
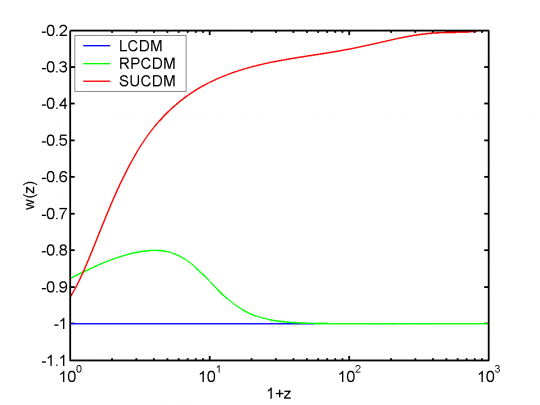
Sélection des modèles de quintessence
Il est essentiel de déterminer avant tout les paramètres cosmologiques qui permettent au sein de chaque modèle de reproduire au mieux les observations cosmologiques. Nous avons procédé tout d’abord à une présélection des modèles cosmologiques vis-à-vis de leur adéquation aux diagrammes de Hubble des supernovae de type Ia (SNLS 1st year data set; P. Astier et al., A& A 447, 31-48 (2006)). Ceci est illustré à la figure 2.
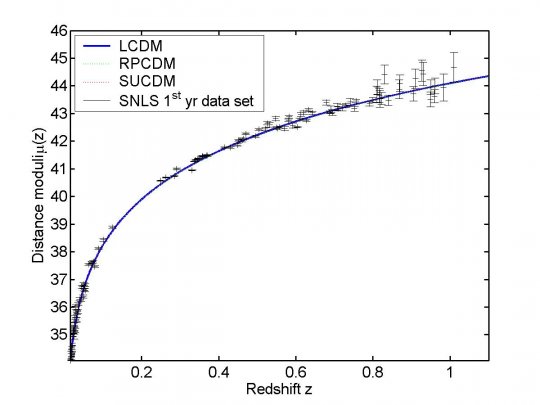
Ensuite, nous avons modifié (en collaboration avec V. Boucher) un code CMB (CAMB) pour tenir compte de la quintessence (cf. aussi P. Brax, J. Martin et A. Riazuelo, Phys. Rev. D 62 103505). Cette étape est essentielle à la fois pour contraindre Omega_b et le s8 dans les modèles de quintessence (voir Fig. 3) mais également pour obtenir le bon spectre de puissance pour les conditions initiales.
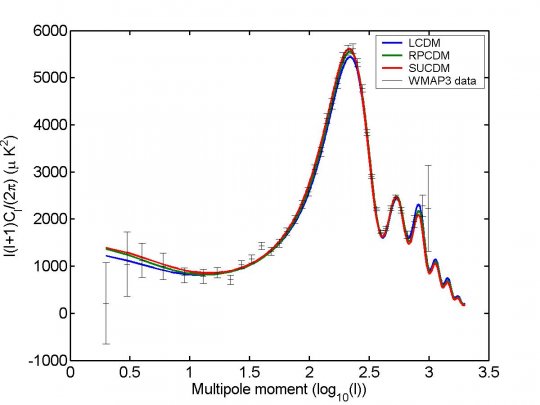
En effet, à des échelles supérieures à 100h^-1 Mpc, l’inhomogénéité du champ de quintessence modifie sensiblement la pente à grande échelle du spectre. De même, par les différences entre les paramètres cosmologiques considérés, les oscillations baryoniques dans le spectre sont différentes entre les modèles (voir Fig. 4).
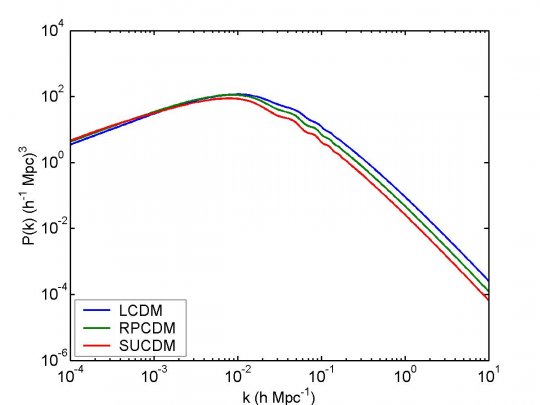
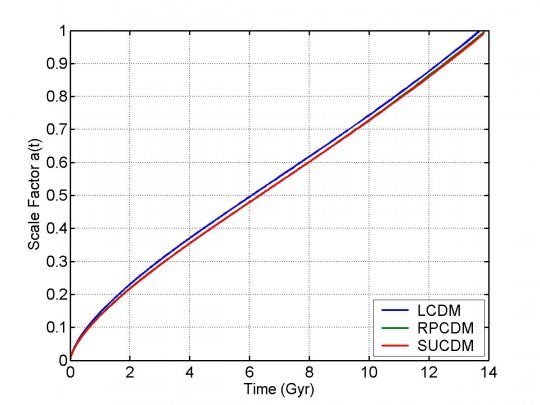
L’évolution cosmologique du facteur d’échelle est représenté à la Figure 5. Enfin, du point de vue de la normalisation, le s8 est différent pour chaque modèle (cf. Fig. 3) et le mode linéaire de croissance des structures est différents. Tout ceci conduit à un a initial différent.
Résumé des modifications apportées par la quintessence
![]() Paramètres cosmologiques différents
Paramètres cosmologiques différents
| Modèles | SUCDM | RPCDM | LCDM |
| h | 0.73 | 0.73 | 0.73 |
| Omega_m | 0.18 | 0.2 | 0.24 |
| Omega_b | 0.042 | 0.041 | 0.042 |
| Omega_v | 0.82 | 0.8 | 0.76 |
| n | 0.951 | 0.951 | 0.951 |
| s8 | 0. 45 | 0.58 | 0.74 |
![]() Spectre de puissance initial différent (grandes échelles - inhomogénéité ; B.A.O. paramètres cosmologiques ; normalisation s8)
Spectre de puissance initial différent (grandes échelles - inhomogénéité ; B.A.O. paramètres cosmologiques ; normalisation s8)
![]() Mode linéaire de croissance des fluctuations (et vitesses)
Mode linéaire de croissance des fluctuations (et vitesses)
![]() expansion cosmique différente durant l’ère de matière
expansion cosmique différente durant l’ère de matière
Note : jusqu’à présent, l’inhomogénéité du champ de quintessence dans le code de formation des structures n’a pas encore été implémenté. Son effet devrait surtout se marquer aux grandes échelles dans le cas des modèles de quintessence tracking.
Simulations numériques
Forts de tous ces éléments, nous avons réalisé des simulations N-corps (Particle-Mesh) avec de la matière noire uniquement mais avec 1024^3 particules et cellulles de grille. Les modèles considérés sont un LCDM de référence (paramètres cosmologiques WMAP3) et les deux modèles cosmologiques introduits ci-dessus. Pour chaque simulation, 65 snapshots ont été sauvegardés entre z(initial) et z=0. Au total, ce sont donc 1.6 To (!) de données générées pour chaque simulation. Ces données sont actuellement stockées à l’IDRIS et seront ramenées sur la méso-grille et la méso-machine d’ici peu. Deux snapshots sont illustrés à la Figure 6 et 7. Une analyse statistique de la boîte devrait déjà donner un .premier critère de discrimination sur le s8 et le B.A.O. (voir analyse CMB)






